Example

We compute $\mathcal{BC}_n(G)$ by two methods and take symmetric group $G=\mathcal{S}_5,n=2$ as an example.

Remark: the group $G$ is of type GrpPerm.

First, we compute $\mathcal{BC}_n(G)$ by definition:

• Open the magma code that computes group $\mathcal{BC}_n(G)$ by definition, copy all lines of code and paste in Magma.
• Let $G=\mathcal{S}_5, n=2$ and compute $\mathcal{BC}_n(G)$:

G:=SymmetricGroup(5);
BC,FullLattice,QuoMap,Generators,IndSet2,RelationBase:=BrutalBC(G,2);

• The result is $\mathcal{BC}_2(G)=(\mathbb{Z}/2)^6 \times \mathbb{Z}/4$.

Then we compute $\mathcal{BC}_n(G)$ by decomposition:

• Open the magma code that computes group $\mathcal{BC}_n(G)$ by decomposition, copy all lines of code and paste in Magma.

• Compute $\mathcal{BC}_n(G)$:

• Type the following code:
  

for i in [1..#Out] do
	if Type(Out[i][1]) eq RngIntElt then
		i,0;
	else
		i,Moduli(Out[i][1]);
	end if;
end for;

S:=[];
for i in [1..#Out] do
	if Type(Out[i][1]) eq RngIntElt then
	else
		S:=S cat Moduli(Out[i][1]);
	end if;
end for;
SequenceToMultiset(S);

We see result:

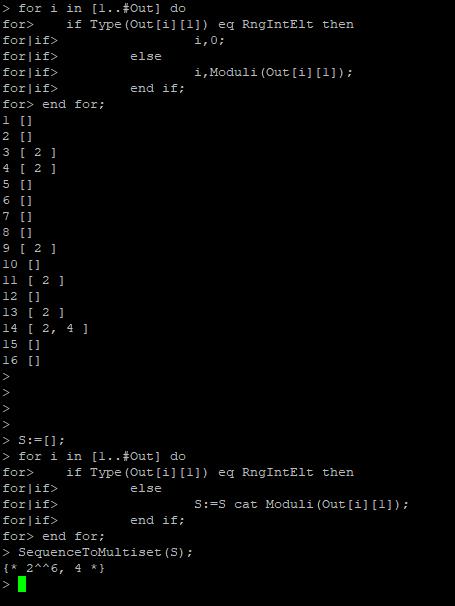
• These two methods give the same result.