Example

We give an example of $G=A_6$ acting on $\mathbb{P}^2$.

• Copy all lines in magma code.
• Input the following code:

  FScale:=CreateBaseFld(SmallGroup(1080,260));
  
  F:=FScale;
  
  sqMin1:=F.1;
  Z3:=F.2;
  Z5:=F.3;
  s:=Z5^2+Z5^3;
  t:=Z5+Z5^4;
  sq5:=2*t+1;
  sq15:=4*sqMin1*Z3*Z5^3 + 4*sqMin1*Z3*Z5^2 + 2*sqMin1*Z3 + 2*sqMin1*Z5^3 + 2*sqMin1*Z5^2 + sqMin1;
  L1:=(-1+sqMin1*sq15)/4;
  L2:=(-1-sqMin1*sq15)/4;
  
  G:=MatrixGroup<3,F|
  [1,0,0, 0,Z5^4,0, 0,0,Z5],
  [-1,0,0, 0,0,-1, 0,-1,0],
  [1/sq5,1/sq5,1/sq5, 2/sq5,s/sq5,t/sq5, 2/sq5,t/sq5,s/sq5],
  [1/sq5,L1/sq5,L1/sq5, 2*L2/sq5,s/sq5,t/sq5, 2*L2/sq5,t/sq5,s/sq5]>;
  

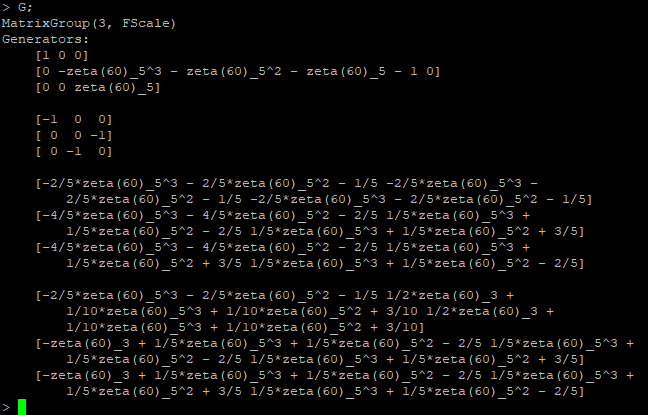
• The group $G=A_6$ has representation as follows:

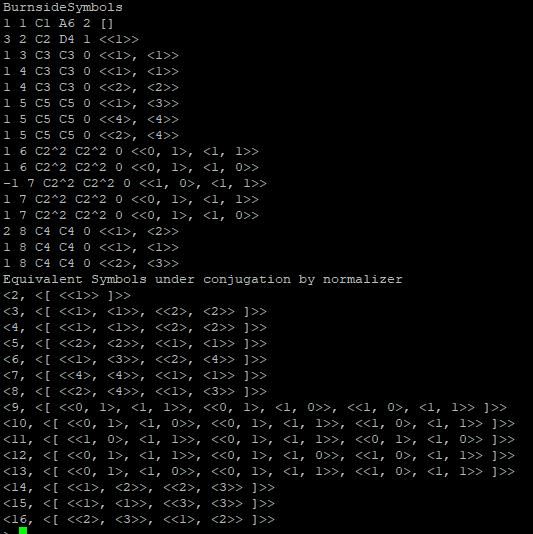
• Use function ComputeBurnsideSymbol(G,F,FScale).

BurnsideSymbols,PG2GHom,G2PGHom,PermG,H,LH,GrpQuo,AllGrp,ChainNode,ChainClass,

ScalarGrp,AllSymbolNGLambda:=ComputeBurnsideSymbol(G,F,FScale);

• The result is as follows,